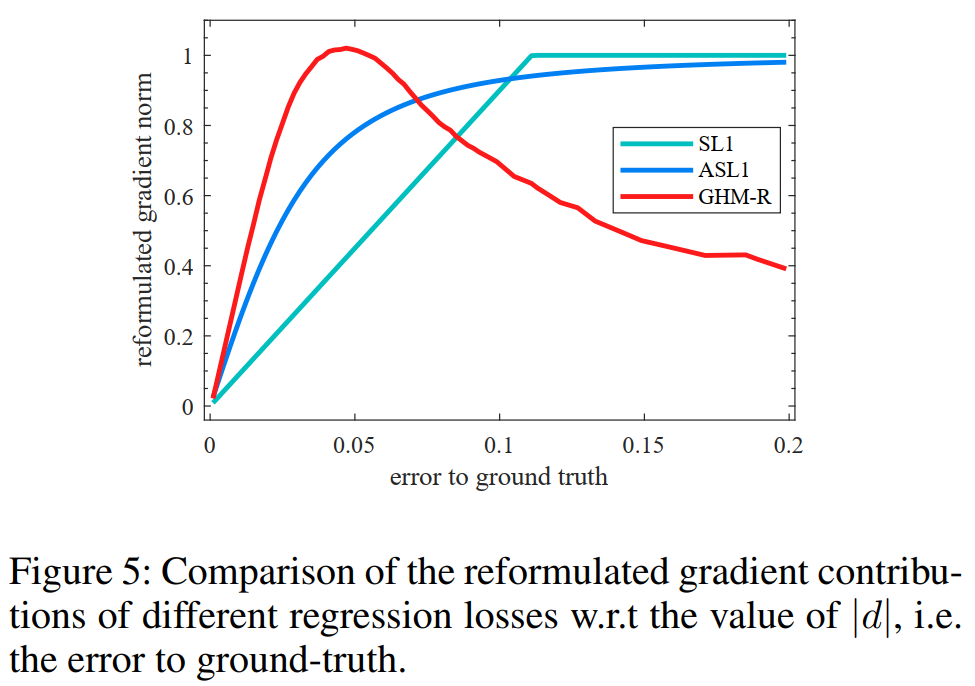
原论文:Gradient Harmonized Single-stage Detector
本文主要基于tf.keras讨论分类部分,论文也提出了适用于检测的方法。
实验表明具有一定效果,可以尝试,感觉比focal loss要好用。
概述
本文针对问题:one-stage的目标检测算法一直存在的正负/难易样本(样本梯度)失衡问题。
在one-stage算法中,负样本的数量要远远大于正样本,而且大多数负样本是简单样本(well-classified);当然,大多正样本也算是简单样本。简单样本的小梯度,通过样本量的增加,量变引起质变,主导了模型的训练过程。focal loss中通过引入大大降低简单样本的分类损失,以平衡正负/难易样本,但是设计的损失函数引入两个超参(OHEM只学习困难/loss大的一部分样本,训练有效性降低):
1 | def focal_loss(y_truth, y_pred, _): |
本论文认为,模型训练过程中,信息/知识的传导靠的是梯度;只不过梯度的大小,表象刚好是样本的难易/正负。也就是说,正负/难易样本的失衡,其实是梯度的失衡!所以想让模型学得更好,应该从更本质的梯度入手。故提出gradient harmonizing mechanism (GHM),拟解决模型中的梯度失衡问题。
我的理解
梯度调和机制(gradient harmonized mechanism, GHM)其实就是将不同梯度对损失函数的影响,进行基于密度的平衡。(如果为了简单了解,我们暂且可以把密度理解为样本数量)
调和机制(harmonized mechanism)
这里把harmonized mechanism翻译为调和机制,其实是调和有取倒数的意思。
基于类别平衡的损失(class-balanced loss)
可以从样本的类别不平衡来理解:如果有10个类的样本,2个类的样本,那么基于类别平衡的损失为:
其中,10可以理解为类别的密度,2可以理解为类别的密度。
推广到多个类别可得:
其中,是样本总数,是样本所属的类别的密度,是样本的损失。以上如果取平均损失函数,则需要乘上。
基于梯度平衡的损失(gradient-balanced loss)
这里,我们将基于类别的平衡推广到基于梯度的平衡:
其中,是样本总数,是样本的梯度,是梯度的密度,是样本的损失。
也就是说,用样本梯度的密度取倒数,乘上样本损失,便可以平衡不同梯度区域的损失。
为什么需要调和
基于类别的平衡,在实际的数据分析场景中,也要case-by-case分析是否适用。那么,基于梯度的平衡是否科学呢?作者给出了下图的解释(图中还包含了cross-entropy和focal-loss的梯度加和方式):
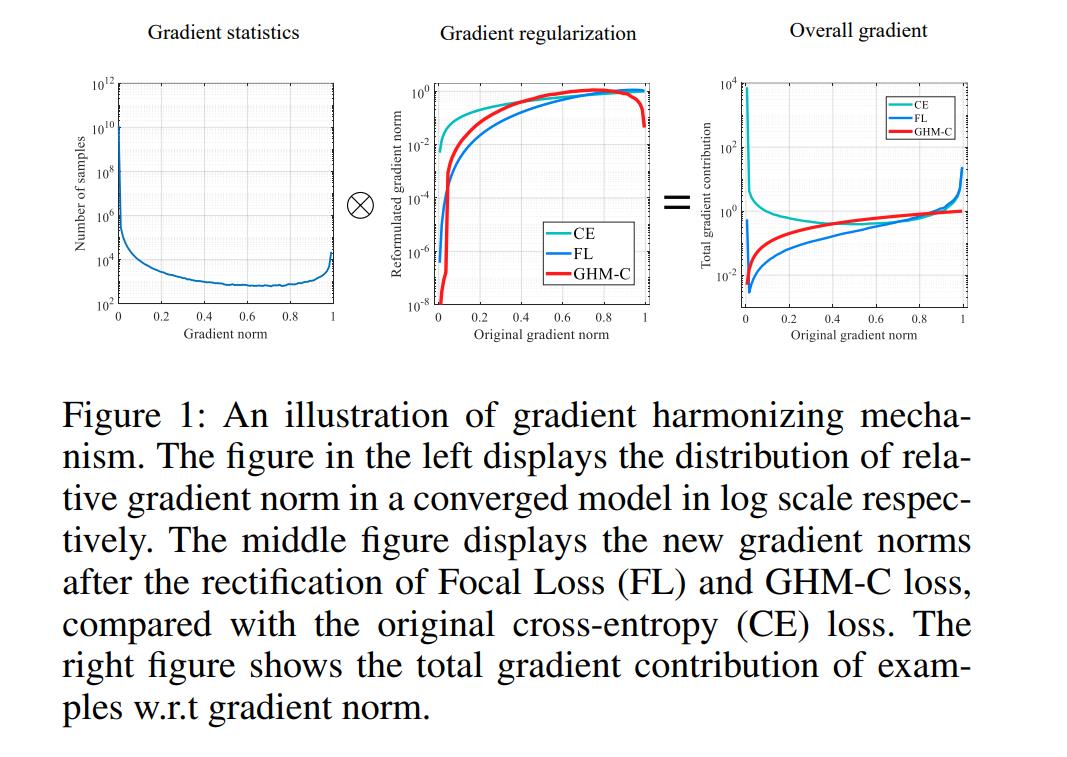
最左边的图是样本的梯度分布,梯度小的表示已经被模型学习到的了(容易样本),梯度大的表示模型很难学到(困难样本)。这两种样本,梯度密度都比较大,主导了整个模型的训练方向。而作者认为,学到的了可以不用学了,没有学到的可能是异常样本,也不用学了;我们这时候应该提升模型,学习中间那段梯度密度较小、还有信息可以学习的样本。
求解出整个样本集梯度的概率密度的调和曲线(1/概率密度,中间那张图),来调和原始的梯度(也就是与左图相乘),得到最终的模型回传梯度(最右边的图)。
和focal loss和OHEM的比较来看,改进源于更本质的角度——模型的梯度(当然,这里的梯度并不是整个模型的所有参数构成的梯度,而是简化为最后一层sigmoid回传的梯度;同时也不是指梯度向量,而是梯度向量的L1范数)。
以上,便是论文的核心理解,接下来掰一掰公式和实现。
Gradient Harmonizing Mechanism —— GHM-C Loss
原论文主要针对的是sigmoid二分类情况,我泛化为softmax来分析。
回过头来看一下GHM的损失函数为:
其中,是batch size,最重要的部分在于求解梯度密度上,
论文通过两个机制来近似这个梯度密度:
- 将梯度取值区间
(0, 1)切割为多个bin,统计不同bin的梯度数量R,作为梯度密度(论文中梯度密度调和参数是); - 用逐
batch的指数加权移动平均(EMA)来近似总样本下的梯度密度。
cross-entropy的损失函数是:
其中,指真实类别概率,预测类别概率为; 代入计算梯度得 (与论文中针对sigmoid的推导结果是一致的):
综上,可得求解GHM-C Loss:
- ;
- 统计( 所在梯度区间的样本数);
- 指数加权移动平均计算;
- 计算梯度密度 ;
- 计算损失 。
1 | def _categorical_ghm_loss(bins=30, momentum=0.75): |
Gradient Harmonizing Mechanism —— GHM-R Loss
一般的回归损失是:
这样得到的梯度为:
由于大部分为梯度为1,没法计算梯度密度。故改进回归损失为:
然后按照 GHM-C Loss 的步骤计算 GHM-R Loss 即可(按经验)。